[마시슬키] 몰드 합성 및 분해 시 합성 구슬 분석
몰드 합성 및 분해 시 합성 구슬을 얼마나 사용/획득하는지 선형회귀를 사용하여 분석
- 목차
서론
배율이 같은 몰드에 대해 합성에 필요한 구슬의 양과 분해해서 얻는 구슬의 양이 다릅니다. 예를 들어, 배율이 10.0인 몰드는 분해할 때 약 1315의 구슬을 얻지만 합성할 때에는 약 500의 구슬을 사용합니다. 배율이 1000인 몰드는 분해할 때 약 35965의 구슬을 얻고 합성할 때에는 약 50000의 구슬을 사용합니다. 낮은 배율에서는 분해할 때 얻는 양이 합성할 때 사용하는 양보다 많지만 높은 배율에서는 합성할 때 사용하는 양이 분해할 때 얻는 양보다 많습니다. 다른 표현으로는, 낮은 배율의 몰드는 높은 배율일 때보다 분해할 때의 효율이 좋습니다.
전투력을 올리려면 몰드를 합성해야겠는데, 그렇다고 무작정 합성만 하기에는 구슬이 없어서 몇몇 몰드는 분해해야 합니다. 어떤 몰드는 분해하고 어떤 몰드는 합성할지 정량적인 기준을 만들어보기 위해 데이터를 수집해보았습니다. 저의 장착하지 않은 몰드와 뽑기를 통해 얻은 몰드의 데이터를 수집했고, 데이터가 복잡하지는 않기 때문에 엑셀을 사용하여 간단하게 정량적으로 분석해보았습니다.
분석
몰드 합성 시 필요한 구슬
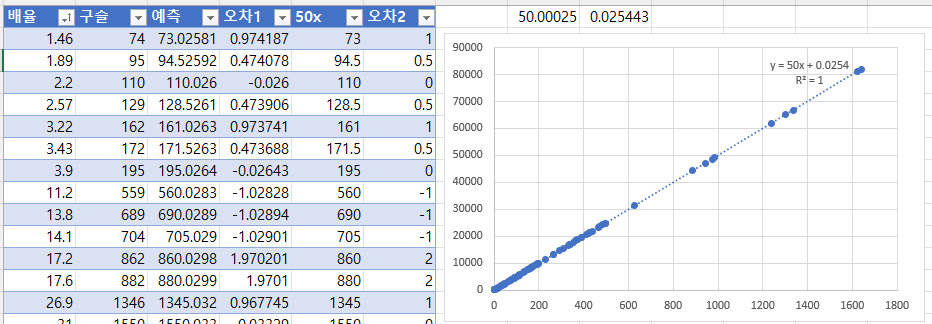 몰드 합성 시 배율에 따른 구슬 소모량 데이터
몰드 합성 시 배율에 따른 구슬 소모량 데이터
먼저 몰드 합성 시 필요한 구슬의 양을 정리했습니다. 엑셀의 LINEST 함수(선형회귀 분석 함수)를 사용하여 분석해본 결과, 위 그림과 같이 $y=50.00025x+0.025443$이라는 결과가 나왔습니다. 위 그림의 표에서
- [배율]은 몰드의 배율
- [구슬]은 해당 몰드를 합성할 때 필요했던 구슬의 양
- [예측]은 LINEST를 통해 얻은 함수를 실제로 적용시켜본 결과
- [오차1]은 [구슬]과 [예측]값과의 차이
- [50x]는 몰드 배율에 50을 곱한 결과
- [오차2]는 [구슬]과 [50x]값과의 차이
입니다.
여기서 다루는 구슬 데이터의 정확도는 1 단위이기 때문에 값을 조금 근사시켜보면 $y=50x$가 됩니다. 따라서 몰드 배율의 50배에 해당하는 구슬이 필요한 것을 알 수 있습니다.
오차는 생길 수밖에 없는데, 게임에서 보여지는 몰드의 배율은 근삿값이기 때문입니다. 게임 상 보여지는 값은 10 미만의 배율에서는 소수점 두 자리, 100 미만에서는 소수점 한 자리, 100 이상에서는 소수점을 보여주지 않습니다. 하지만 시스템 상으로는 그 값이 엄연히 존재하고, 그로 인해 게임에서 같은 배율을 가진 것으로 보여도 합성/분해 시 소모/획득 구슬량이 다른 경우가 생깁니다. 예를 들어, 배율이 150인 몰드는 실제로는 149.5~150.5 사이의 값을 가지게 된다는 것입니다. 따라서 배율이 150인 몰드는 합성 시 7475~7525의 구슬을 사용하게 됩니다. 배율이 150으로 같은 몰드가 두 개 있을 때 합성 시 필요한 구슬의 양은 각각 7487, 7514과 같이 다를 수 있다는 것입니다.
이러한 오차를 감안한다면, 몰드를 합성할 때 (배율)*50의 구슬을 소모한다는 결론은 참으로 볼 수 있겠습니다.
몰드 분해 시 얻는 구슬
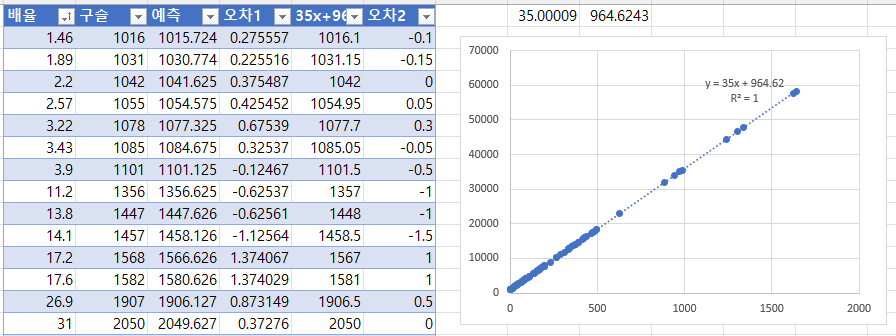 몰드 분해 시 배율에 따른 구슬 획득량 데이터
몰드 분해 시 배율에 따른 구슬 획득량 데이터
합성과 마찬가지로 LINEST 함수를 사용하여 분석해보았습니다. 선형회귀 결과 $y=35.00009x+964.6243$이 나왔습니다. 표의 데이터는 아래와 같습니다.
- [배율]은 몰드의 배율
- [구슬]은 해당 몰드를 분해할 때 얻는 구슬의 양
- [예측]은 LINEST를 통해 얻은 함수를 실제로 적용시켜본 결과
- [오차1]은 [구슬]과 [예측]값과의 차이
- [35x+965]는 몰드의 배율에 35를 곱하고 965를 더한 결과
- [오차2]는 [구슬]과 [35x+965]값과의 차이
마찬가지로 반올림을 해보면 y=35x+965입니다. 오차도 합성에서와 같은 이유로 발생하므로 이 수식도 맞다고 볼 수 있습니다.
숫자의 의미
그런데 여기서 의문점이 하나 생깁니다. “왜 하필 965인가?” 그 정확한 이유는 개발자님만 알겠지만 제가 추측해보기로는 몰드의 배율 때문일 것입니다. 몰드는 1보다 작은 값을 가질 수 없습니다. 기본 몰드가 배율 1로서 발생할 수 있는 가장 작은 값을 가집니다. 이에 준하는 수준의 몰드를 분해했을 때 기본값을 주는 것이 맞지 않겠느냐는 생각이 있었을테고, 그 기본값이 1000이었다면 설명이 가능합니다. 배율이 1인 몰드를 분해했을 때 1000의 구슬을 얻고, 배율이 증가할수록 그 증가량의 35배만큼 구슬을 얻게 된다면, 그 결과를 도출하는 식은 y=35(x-1)+1000이 됩니다. 풀어보면 y=35x+965로 위에서 구한 식과 같은 것을 확인할 수 있습니다.
결론
합성 시에는 (배율)*50의 구슬을 소모, 분해 시에는 (배율-1)*35+1000의 구슬을 획득합니다. 이를 바탕으로 그래프를 그려보면 아래와 같이 됩니다.
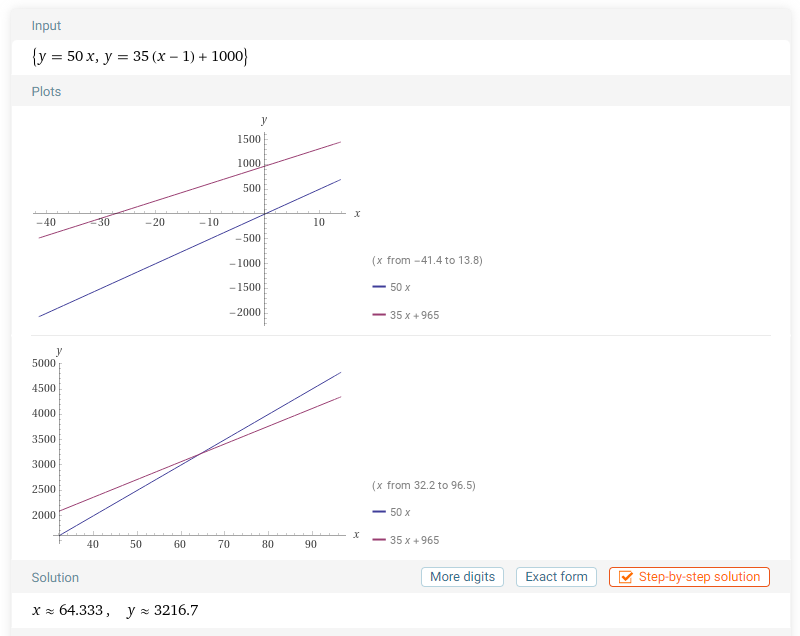
두 그래프가 만나는 지점은 배율이 약 64.3일 때입니다. 이 지점 이후로는 몰드 분해를 통해 얻는 구슬의 양보다 합성할 때 사용하는 구슬의 양이 많다는 것을 알 수 있습니다.
다만, 이 분석의 결과는 64.3 이하의 몰드는 분해하고 64.3 이상의 몰드는 합성하는 것이 효율적이라는 결론을 내지 못합니다. 몰드 합성/분해에 있어서 효율적이라는 것은, 구슬이 부족하거나 넘치지 않는 상태를 유지하면서 분해 및 합성을 원할 때 할 수 있는 것이라 할 수 있겠습니다. 즉, 구슬의 획득량과 소모량의 균형이 맞는 상태인 것입니다. 이 상태를 판단하려면 특정 배율의 몰드가 얼마나 나오는지에 대한 데이터도 필요합니다. 그 데이터와 위에서 구한 데이터를 통계학적으로 분석해야만 효율성을 판단할 수 있습니다. 이 글에서 분석한 데이터는 각 개인마다 어떤 배율의 몰드를 합성하고 분해할지에 참고할 수 있는 수치 이상의 의미는 가지지 못합니다. 따라서 기준을 정할 때 이 데이터는 참고만 하되 직접 합성/분해를 해보며 기준을 조정하는 것이 좋습니다.