Dynamix의 보상 Frag를 구하는 공식이 있을까? - 1 (엑셀을 사용한 추론)
소량의 데이터와 엑셀을 사용하여 Frag 공식의 대략적인 형태를 분석한다.
- 목차
홍콩의 게임 개발사인 C4Cat에서 제작한 리듬게임 Dynamix는 이벤트 모드를 플레이할 시 게임 결과에 따라서 Frag라는 게임 내 재화를 지급한다. 이런 식으로 지급하는 재화는 결과에 따라 어느 정도를 주어지는지에 대한 공식이 있기 마련인데, 이 Frag의 공식에 대해서는 알려진 바가 없다. 그나마 알려진 것은 나무위키의 🔗Dynamix 문서에서 찾아볼 수 있는데, 만점을 받았다는 가정 하에 플레이한 레벨에 따라 $5L^2+31L+410$의 Frag를 얻을 수 있다고 나와있다. 또한 11레벨 이상의 난이도에서는 맞아떨어지고 10레벨 이하에서는 상수항을 2, 5레벨 이하에서는 상수항을 4만큼 빼서 계산하라고 나와있다. 그리고 레벨 클리어에 실패한 경우는 고정적으로 40 Frag를 얻을 수 있다고 한다. 하지만 진행한 난이도와 얻은 점수에 따라 정확히 얼마의 Frag를 얻을 수 있는지에 대해서는 나와있지 않았다. 그래서 이 공식을 정확히 얻을 수 있게 만들어보고 싶은 생각에 이걸 시작했다.
<이벤트 모드 플레이 시 결과 화면 예시. 위의 2070이 획득한 Frag이다>
데이터 수집(수동)
이 공식을 얻으려면 실제 데이터를 통해 공식을 추측하는 과정이 필요한데, 이 데이터를 얻을 수 있는 방법은 직접 플레이하는 것과 트위터에서 다른 사람의 결과를 가져오는 것이 있다. 이 결과를 레벨 별로 분류하여 엑셀에 점수와 Frag를 정리하고 규칙을 찾았다.
직접 플레이하는 것은 별다른 설명이 필요없으므로 생략하고, 트위터에서 다른 사람의 데이터를 사용하는 것은 다음과 같다. 트위터에는 Dynamix의 결과 공유 기능을 사용하여 플레이 결과를 게시하는 사람들이 있고, 그 중에서도 이벤트 모드의 결과를 게시하는 사람들이 있다. 이벤트 모드의 결과를 게시하면 이벤트 모드를 통해 얻은 Frag의 양도 같이 표시가 되는데, 이것을 수집하여 데이터로 사용할 수 있겠다는 생각이 들었다. 이를 위해 트위터 검색창에서 #dynamix로 검색하여 트위터에 올라온 이미지를 검색했다. 이 이미지를 모두 확인하면서 이벤트 모드인 것만 골라 그 결과를 엑셀에 정리했다.
<트위터 검색 예시, 특정 기간의 오메가 기록만 확인하는 쿼리>
알려진 바로는 플레이한 채보의 난이도와 점수에 따라서 Frag가 결정된다고 하지만, 혹시 모를 경우를 대비해 가능하면 세부 판정 결과(Perfect, Good, Miss, Max Combo)도 같이 정리하기로 했다. 직접 플레이한 경우는 Frag와 세부 판정을 모두 볼 수 있으므로 정리하고, 트위터에서 가져온 데이터는 Frag나 세부 판정 둘 중 하나만 볼 수 있기 떄문에 Frag만 정리했다.
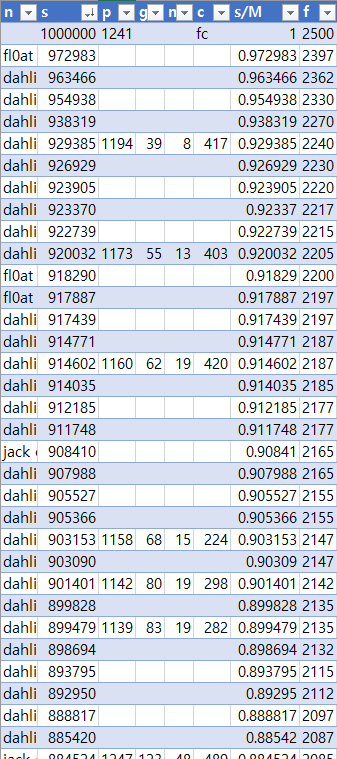
<40개 정도의 15레벨 데이터>
Frag 값이 다양
데이터를 수집하다보니 경우에 따라 Frag의 값이 다른 것을 알 수 있었다. 이렇게 되는 이유는 아래와 같이 몇 가지가 존재한다.
- 상점에서 구입할 수 있는 Frag 2배 버프
- 이벤트로 일정 기간 제공하는 Frag 1.5배 버프
- 특정 날짜를 기점으로 제공하는 Frag의 양이 1.25배 영구 증가
마지막 요인인 1.25배 영구 증가로 인해 현재는 클리어 실패 시 받는 Frag가 40이 아니라 50이고, 15렙 기준 오메가 달성 시 Frag도 2000이 아닌 2500이다. 다만 15레벨의 데이터를 관찰해본 결과 1의 자리가 0, 2, 5, 7밖에 없는 것으로 보아 증가되기 전 Frag는 항상 짝수만 나오고, 증가된 후에는 이 값에 1.25배를 한 후 소수점 아래는 버리는 것으로 판단되어 공식을 만들 때에는 보다 더 패턴이 있는 영구증가 이전 값에 대해서 만들기로 했다.
경향성 추론을 위한 가정과 변수 설정
우선 Frag 값에 영향을 주는 인자가 점수(s)와 레벨(l)이므로 다음과 같이 Frag값을 반환하는 함수를 정의한다.
\[F(s,l)=\Sigma(s)\Lambda(l)+C\]가정
모든 레벨의 데이터를 본 결과 영구증가 이후의 Frag값의 1의 자리가 0, 2, 5, 7만 존재함을 확인했다. 즉, 영구증가 이전의 Frag 값의 1의 자리는 짝수인 것이다. 하지만 충분한 데이터를 모으지 못했기 때문에 그렇다고 확정은 할 수 없고, 영구증가 이전의 Frag 값은 항상 짝수라는 가정만 하겠다. 또한 이 사실을 통해 소수점 아래는 모두 버린다는 가정도 할 수 있는데, 영구증가된 Frag의 1의 자리가 0, 3, 5, 8이 아닌 0, 2, 5, 7인 것에서 추론할 수 있다. 영구증가하여 xxx2.5와 xxx7.5가 된 것을 반올림하지 않고 그대로 버려야 1의 자리가 0, 2, 5, 7이 되기 때문이다.
이벤트 모드에서 플레이 도중 체력이 부족해서 클리어에 실패하는 경우가 있는데, 이 때는 Frag를 기본값인 40만큼 지급한다. 따라서 점수가 0인 경우 레벨에 상관없이 $F$의 값이 40이 되도록 하는 것으로 간주한다. 이 때문에 위의 식에서 상수항 C가 들어간다. 레벨에 상관없이 F가 일정한 값이 나오게 하려면 $\Sigma(0)=0$이어야 하는데, 상수항이 없다면 F의 값이 항상 0이 나오게 된다. 그러므로 상수항 $C=40$을 추가해준다.
정말 수학을 좋아하는 개발자/기획자가 있는 것이 아닌 이상 복잡한 식은 사용하지 않을 것이다. 그래서 $\Sigma$와 $\Lambda$는 다항함수일 것이라 예상했다. 여기에 나무위키에서 만점일 때의 Frag가 이차함수의 꼴로 주어졌다고 했기 때문에 $\Lambda(l)$가 이차함수일 것이라 추측했다.
점수에 대한 Frag의 경향성 추론을 위한 변수 설정 및 추론
이제 엑셀에 정리한 데이터를 바탕으로 경향성을 확인할 수 있는 몇 개의 계산식을 정했다. 점수를 x좌표, Frag를 y좌표로 해서 그래프를 그린 후 각각 만점, 영점, 최소점으로부터 직선을 그었을 때 기울기의 생김새를 보고 공식을 예측하기로 했다. 15레벨에서의 그래프는 아래와 같았다.
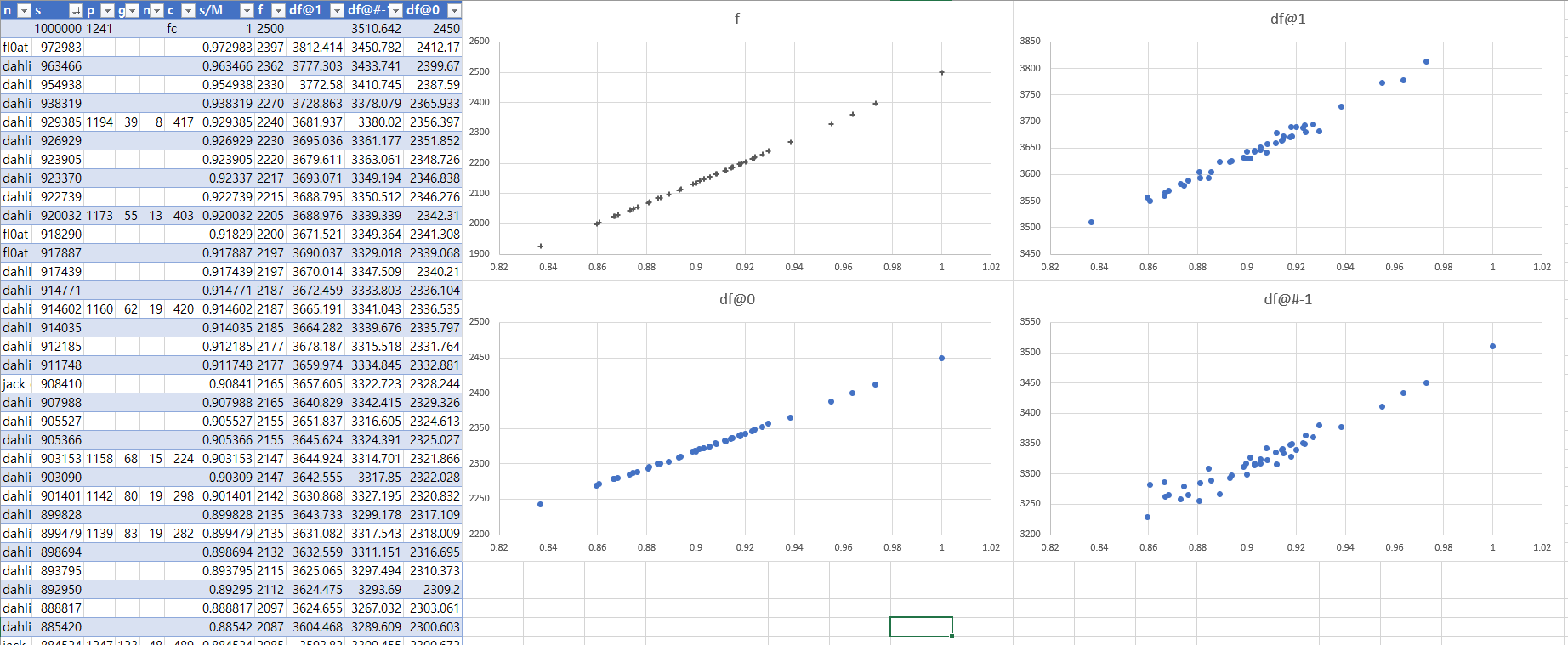
<15레벨 데이터를 좌표평면에 표시한 그래프>
사용할 변수는 다음과 같다.
f: 플레이한 결과로 얻은 Frag의 참값df@0: 영점으로부터 이 결과에 해당하는 점에 직선을 그었을 때 그 직선의 기울기df@1: 만점으로부터 이 결과에 해당하는 점에 직선을 그었을 때 그 직선의 기울기df@#-1: 데이터 중 가장 점수가 낮은 점으로부터 이 결과에 해당하는 점에 직선을 그었을 때 그 직선의 기울기
점이 찍힌 양상을 보면 df@0는 고르게 분포한 반면, df@1와 df@#-1은 다소 편차가 큰 것으로 보인다. 이것은 Frag가 항상 정수인데 이것을 기준으로 기울기를 잡으려고 하니 오차가 크게 발생하는 것이며, 기준점에 가까울수록 더욱 큰 오차가 생기는 것을 볼 수 있다. 종합적으로 보면 df@1와 df@#-1의 데이터는 다소 신뢰하기 힘들며, 그나마 개형이 부드러운 df@0에 해당하는 점들은 선형에 가까운 모습을 보이는 것을 알 수 있다. 그리고 그에 따라 시트에서의 f, 공식에서의 $\Sigma$는 이차함수일 것이라 예측해볼 수 있다. 이제 엑셀의 추세선 기능을 사용하여 점수의 경향성을 알아보겠다.(아래의 그림은 영구증가되기 이전 값에 대한 데이터이고 영구증가된 값은 0.8배 후 버림하여 영구증가 전 값으로 변환했다)
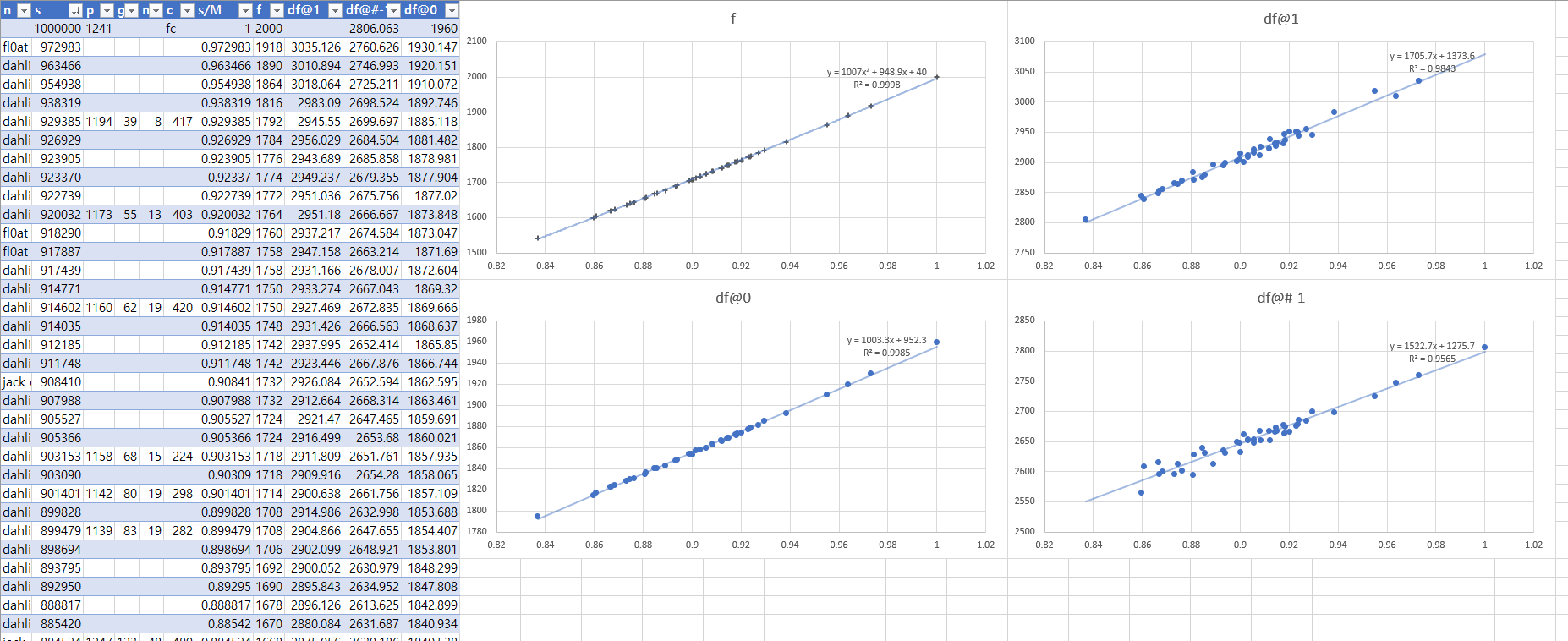
<df에 1차, f에 2차 추세선(y절편 40)을 적용한 모습>
자세히 보면 f는 R2값이 0.9998, df@0는 0.9985으로 나름 준수한 식을 얻었음을 알 수 있다. 하지만 이 추세선을 사용하여 만점에 대한 Frag를 구하면 1995.xxx로 크게 차이가 난다. 조금 더 정확성을 높이기 위해 추세선의 차수를 하나 더 높여보겠다.
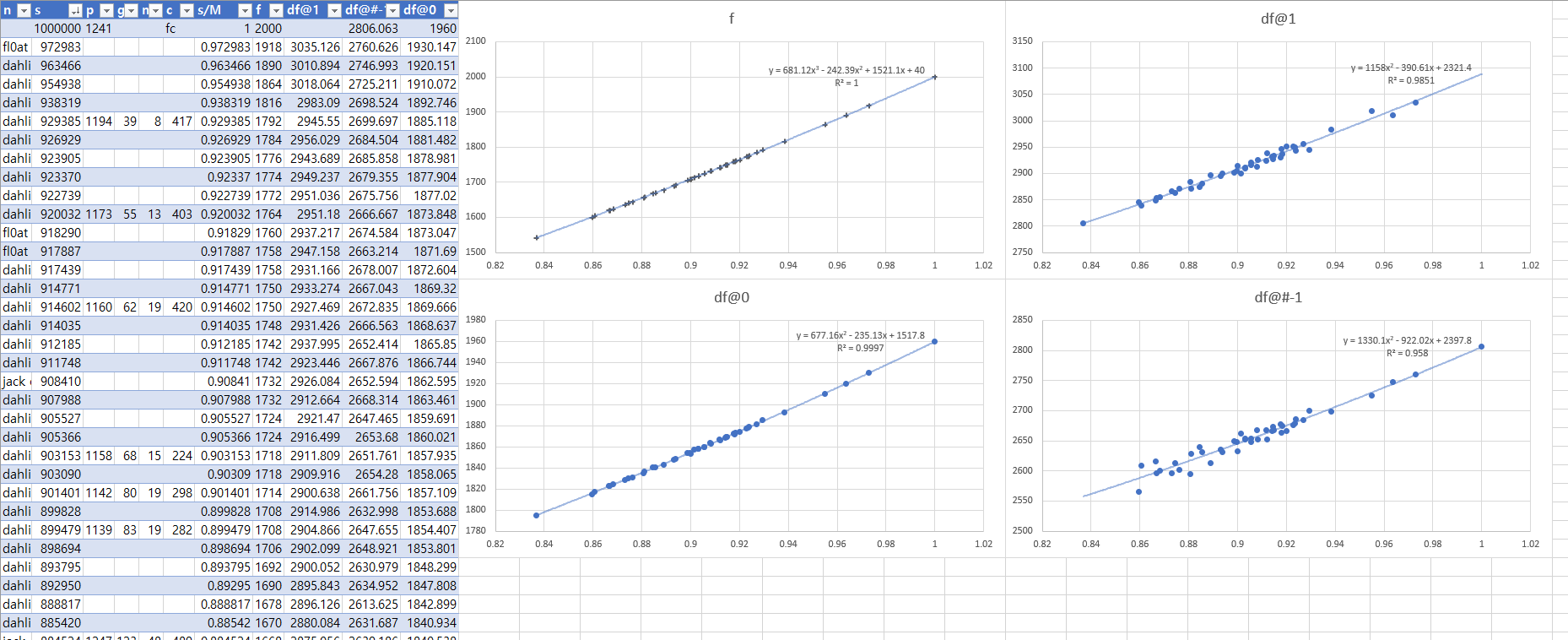
<df에 2차, f에 3차 추세선(y절편 40)을 적용한 모습>
이제 R2 값이 f는 1, df@0는 0.9997로 거의 들어맞는 수준에 도달했음을 알 수 있다. 실제로 만점에 대한 Frag를 구하면 1999.846으로 매우 유사하게 값이 나옴을 알 수 있다. 이렇게 얻어진 추세선으로 현재까지의 15레벨 데이터의 frag를 예측해보면 실제값과 최대 0.95의 오차를 가지게 된다. 이를 통해 Frag의 양은 점수의 삼차함수에 비례한 값으로 주어진다고 추정해볼 수 있다.
레벨에 대한 경향성 추론
오메가가 아닌 점수에 대해서는 정확히 같은 점수를 만들기 힘드므로 각 레벨에 대하여 만점인 기록을 사용해서 레벨에 따른 Frag를 정리했다.
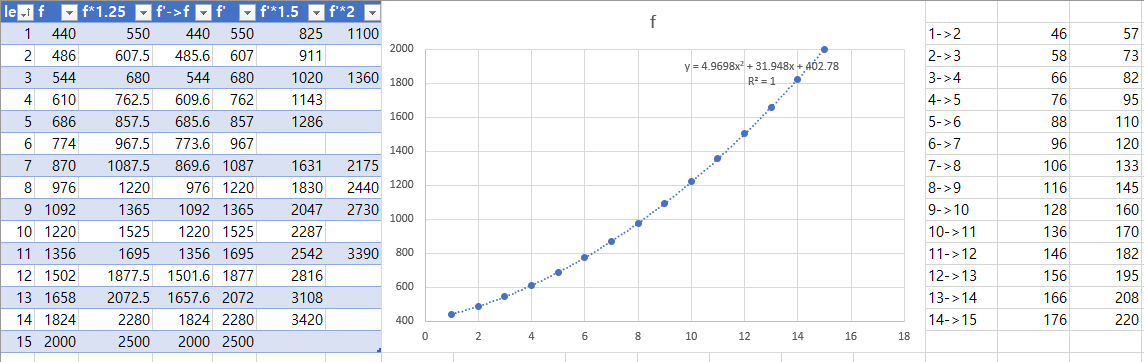
<레벨 별 만점 시 Frag 및 차이>
그래프에 이차함수 형태의 추세선을 그렸는데, 이 때의 R2값이 1로 잘 나왔다. 하지만 인접 레벨 간 Frag 차이값(그래프 우측, 각각 증가 전 / 증가 후)을 보면 대부분 일정한 증가폭을 보이나 특정 구간에서는 증가값이 기존 패턴보다 약간 더 크다. 이를 통해 두 가지 경우를 예상해볼 수 있다.
- 레벨 별로 만점 시 Frag가 고정값으로 정해져있고 여기에 점수에 따른 배율이 곱해진다. 즉, $\Lambda(l)=\lambda_l$의 수열로 표현되고 그 관계식은 따로 없다.
- 레벨에 따른 만점 시 Frag가 특정 함수로 기술될 수 있고 여기에 점수에 따른 배율이 곱해진다. 엑셀에서 분석한대로 이차함수이거나 다른 함수가 존재하여 $\Lambda(l)$을 표현할 수 있다.
추론 결과
Frag가 짝수라는 가정(또는 추정)으로 인하여 $F(s,l)=\Sigma(s)\Lambda(l)+40$이었던 공식을 $F(s,l)=2\cdot\text{int}(\frac{\Sigma(s)\Lambda(l)}{2})+40$으로 고칠 필요가 있다. 여기서 int 함수는 버림, 올림, 또는 반올림하는지 여부를 모르는 가까운 정수로 변환하는 미지의 함수를 의미한다.
레벨을 고정시켜놓고 점수에 따른 Frag 값을 분석한 결과 점수에 따른 영향은 삼차함수일 확률이 높았고, 점수를 만점으로 고정시켜놓고 레벨에 따른 Frag 값을 분석한 결과 레벨에 따른 영향은 이차함수이거나 수열일 확률이 높았다. 다음 포스트부터는 이 두 가지의 경우를 모두 고려하여 계산을 해보고, 가능하면 $\Lambda$를 함수인 방향으로 유도해보겠다.